Building Meshes

When trying to build a 3D model of an object in the real world, the goal is most often to construct a connected mesh of triangles or quadrilaterals that represents that object's surface. When we're using lidar or a stereo camera to collect 3D information, however, we can't create this mesh directly. The data comes to us in the form of discrete points in space, and we have to infer how those points ought to be connected to form a continuous surface.

This is a challenging problem that has inspired a lot of research over the last few decades, but that research has coalesced into some excellent tools. Open3D, for instance, has three different surface reconstruction algorithms built in by default, and of those, Poisson surface reconstruction works extremely well. Nothing is a silver bullet, though, and we still occasionally have specific needs that aren't perfectly well-served by any of the off-the-shelf algorithms.

At my day job, I work on a team that identifies products one would normally find in a convenience store. We use RGBD cameras which supply a point cloud of the scene, and we want to find meshes for each individual product.¹ More specifically, we want a mesh that represents what the real world is like. That means that no part of the mesh intersects itself, each edge bounds exactly two faces, and there's an unambiguous "inside" and "outside" of the surface.² If we have all of these characteristics, we can do things like calculate the volume of an object fairly accurately or even translate or rotate objects in a scene to create new synthetic images for training machine learning models.

While the real world contains some complicated shapes, convenience store products tend to be pretty simple. Water bottles, candy bars, bags of chips, and canned drinks are all mostly convex with no holes. The Open3D surface reconstruction algorithms we referenced before are able to create surfaces that are very accurate, but they don't always give us a mesh that meets all of our "real world" criteria above. We can illustrate this by building a mesh using both ball pivoting and Poisson reconstruction from points sampled from the Stanford bunny.

import open3d as o3d

bunny = o3d.data.BunnyMesh()
mesh = o3d.io.read_triangle_mesh(bunny.path)

# Prettify the mesh for visualization.
mesh.compute_vertex_normals()
mesh.paint_uniform_color([0.5, 0.5, 0.5])

o3d.visualization.draw_geometries([mesh])

The original mesh is quite detailed, but we'll take a smaller subset of points on the surface to use for testing.

def get_bunny_point_cloud(
    number_of_points: int = 5000, visualize: bool = False
) -> o3d.geometry.PointCloud:
    bunny = o3d.data.BunnyMesh()
    mesh = o3d.io.read_triangle_mesh(bunny.path)

    pc = mesh.sample_points_poisson_disk(
        number_of_points=number_of_points, init_factor=5
    )

    if visualize:
        o3d.visualization.draw_geometries([pc])

    return pc

bunny_pc = get_bunny_point_cloud(visualize=True)

Ball Pivoting

We can first try ball pivoting using roughly the example code from the Open3D documentation.

def build_mesh_with_ball_pivoting(
    pc: o3d.geometry.PointCloud, visualize: bool = False
) -> o3d.geometry.TriangleMesh:
    radii = [0.005, 0.01, 0.02, 0.04]

    mesh = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(
        pc, o3d.utility.DoubleVector(radii)
    )

    # Prettify the mesh for visualization.
    mesh.compute_vertex_normals()
    mesh.paint_uniform_color([0.5, 0.5, 0.5])

    if visualize:
        o3d.visualization.draw_geometries([mesh])

    return mesh

ball_pivoting_mesh = build_mesh_with_ball_pivoting(bunny_pc, visualize=True)

The newly constructed surface is clearly similar to the original, which is a good sign. On the original Stanford bunny, there were holes in the bottom of the mesh, presumably because the bunny was resting on something during scanning. When we look at the bottom of our reconstructed mesh, we see that these holes are mostly filled in, but there are still a couple of small gaps in the mesh.

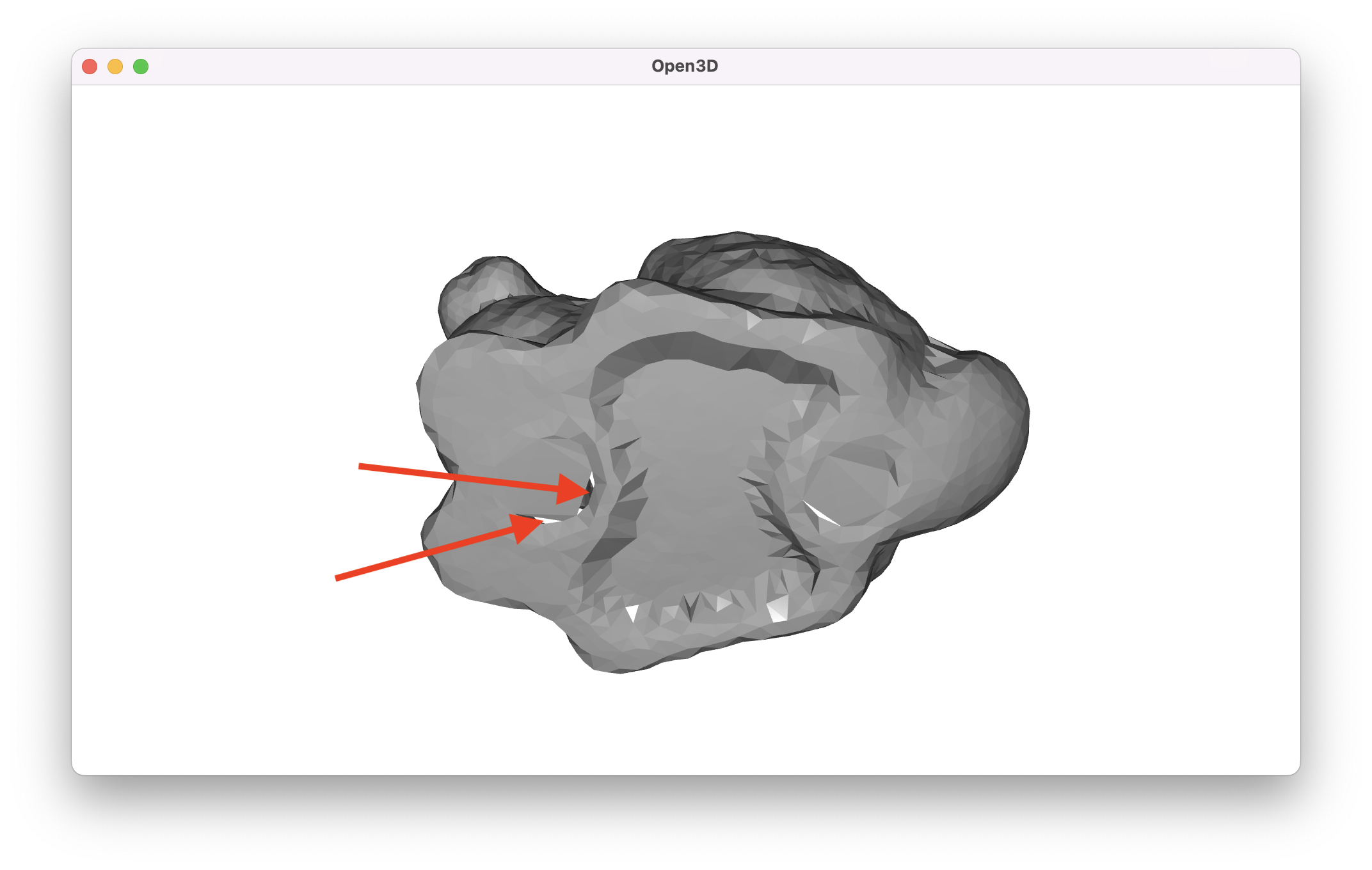
It's not unreasonable to say that we're nitpicking when we point out these tiny, easily correctable gaps. However, it's important to realize that the point cloud we're working with is about as idyllic as possible. Real world data often has noise, variable point density, and large gaps. We can simulate some of those gaps by chopping off some of the points from the top and bottom of our bunny.

import numpy as np

aabb = bunny_pc.get_axis_aligned_bounding_box()

max_bound = aabb.get_max_bound()
min_bound = aabb.get_min_bound()
difference = max_bound - min_bound

new_max_bound = np.array(
    [
        max_bound[0],
        max_bound[1] - difference[1] * 0.2,
        max_bound[2],
    ]
)
new_min_bound = np.array(
    [
        min_bound[0],
        min_bound[1] + difference[1] * 0.2,
        min_bound[2],
    ]
)
shrunk_aabb = o3d.geometry.AxisAlignedBoundingBox(new_min_bound, new_max_bound)

cropped_bunny_pc = bunny_pc.crop(shrunk_aabb)

build_mesh_with_ball_pivoting(cropped_bunny_pc, visualize=True)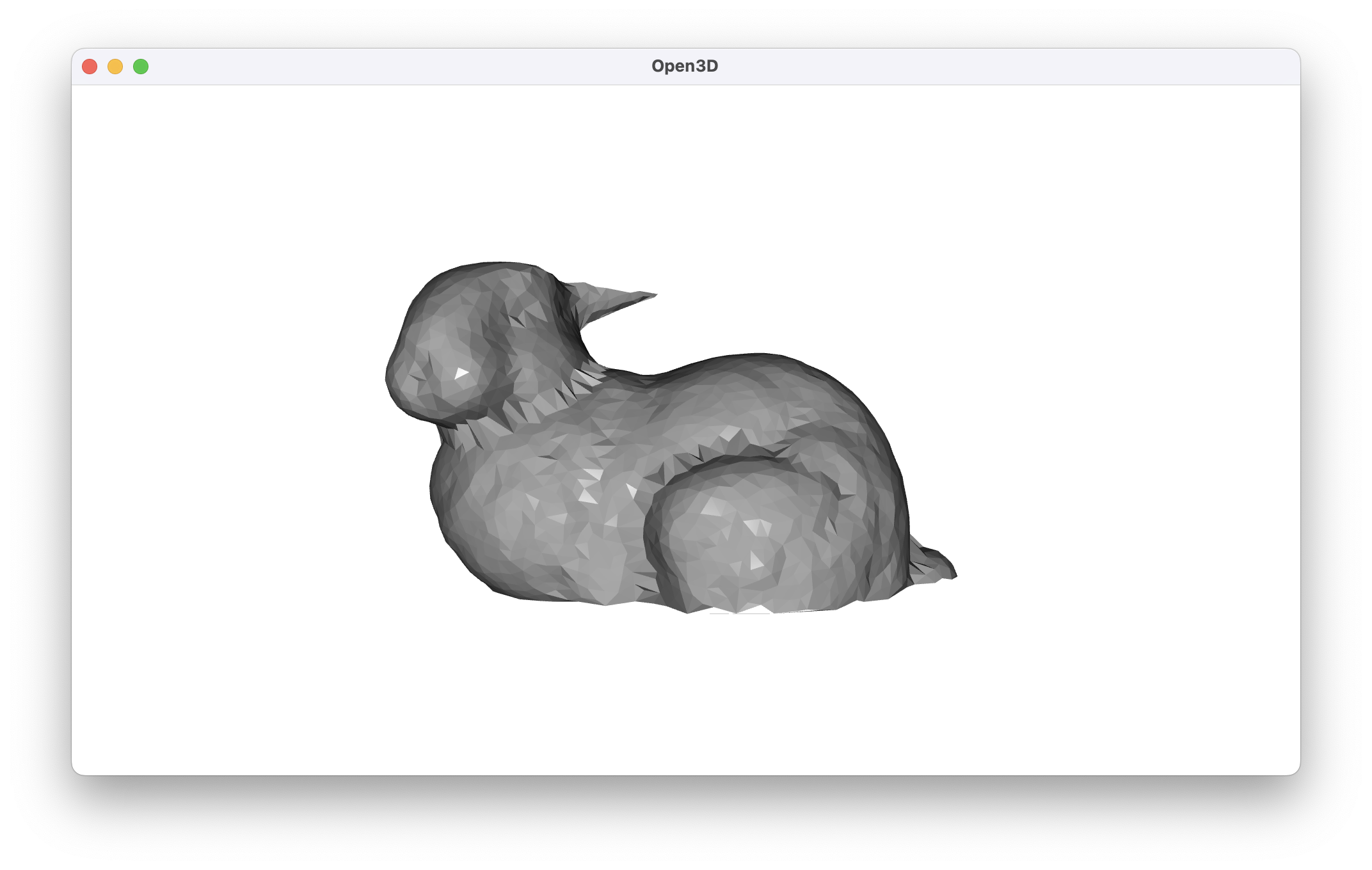

As we can see, ball pivoting is no longer able to span the large gaps we've formed. Even though this is a contrived example, the algorithm's parameters would have to be carefully tuned to span our newly created gaps in the feet and ears of the bunny. If we know that our object's surface should be "closed" despite gaps in the data, this won't get us there very easily.

Poisson Surface Reconstruction

Poisson surface reconstruction is significantly more sophisticated than ball pivoting, and in general, it should be one's go-to tool for rebuilding surfaces. When we try it on our original bunny point cloud, the surface is excellent, though we're still working from very ideal test data.

def build_mesh_with_poisson(
    pc: o3d.geometry.PointCloud, visualize: bool = False
) -> o3d.geometry.TriangleMesh:
    mesh, densities = o3d.geometry.TriangleMesh.create_from_point_cloud_poisson(
        pc, depth=9
    )

    mesh.compute_vertex_normals()  # For shading
    mesh.paint_uniform_color([0.5, 0.5, 0.5])

    if visualize:
        o3d.visualization.draw_geometries([mesh])

    return mesh

build_mesh_with_poisson(bunny_pc, visualize=True)

In the cropped case, Poisson is able to close the holes in the ears without too much difficulty, but the gap in the bottom of the bunny persists.

build_mesh_with_poisson(cropped_bunny_pc, visualize=True)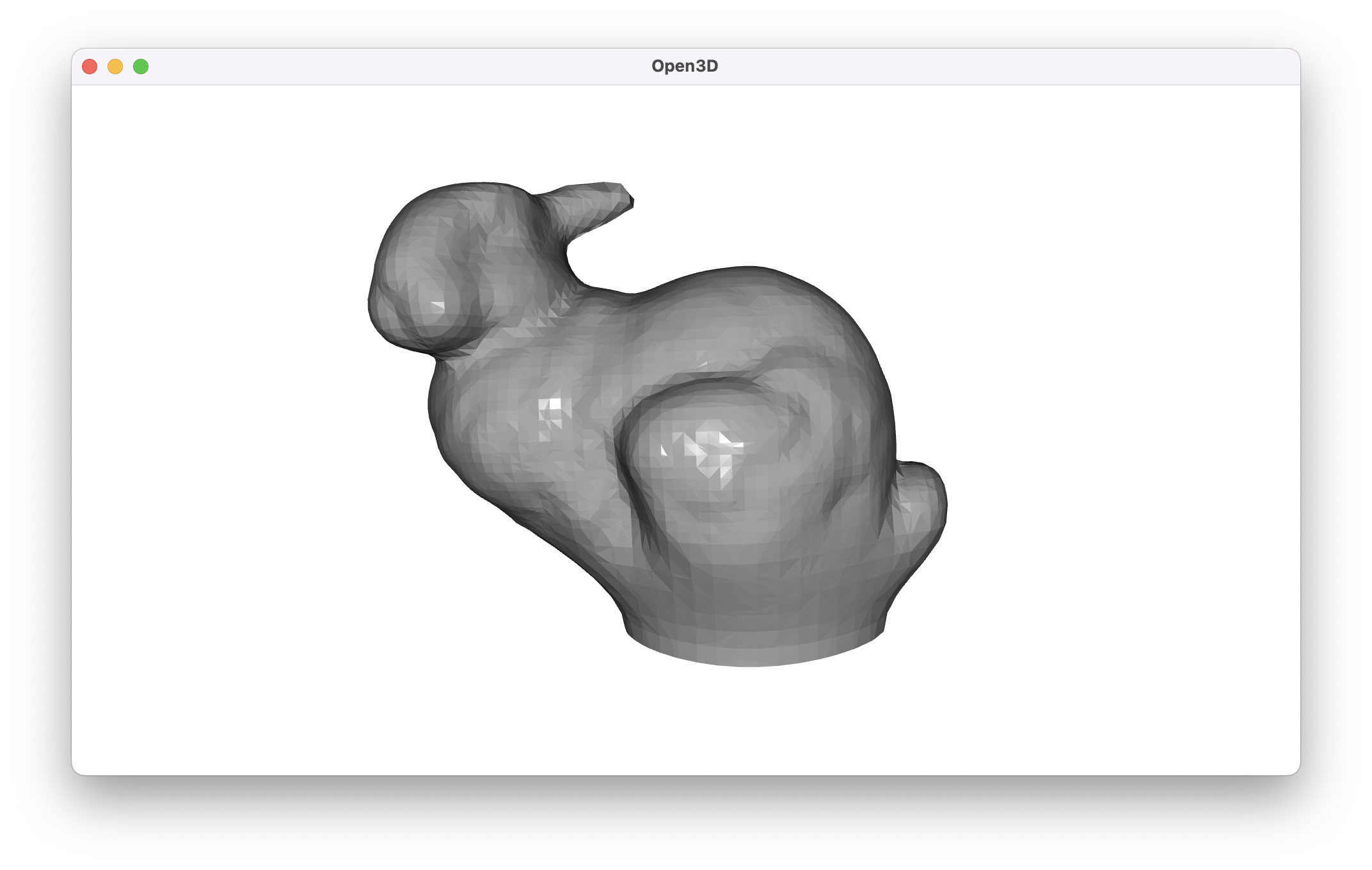

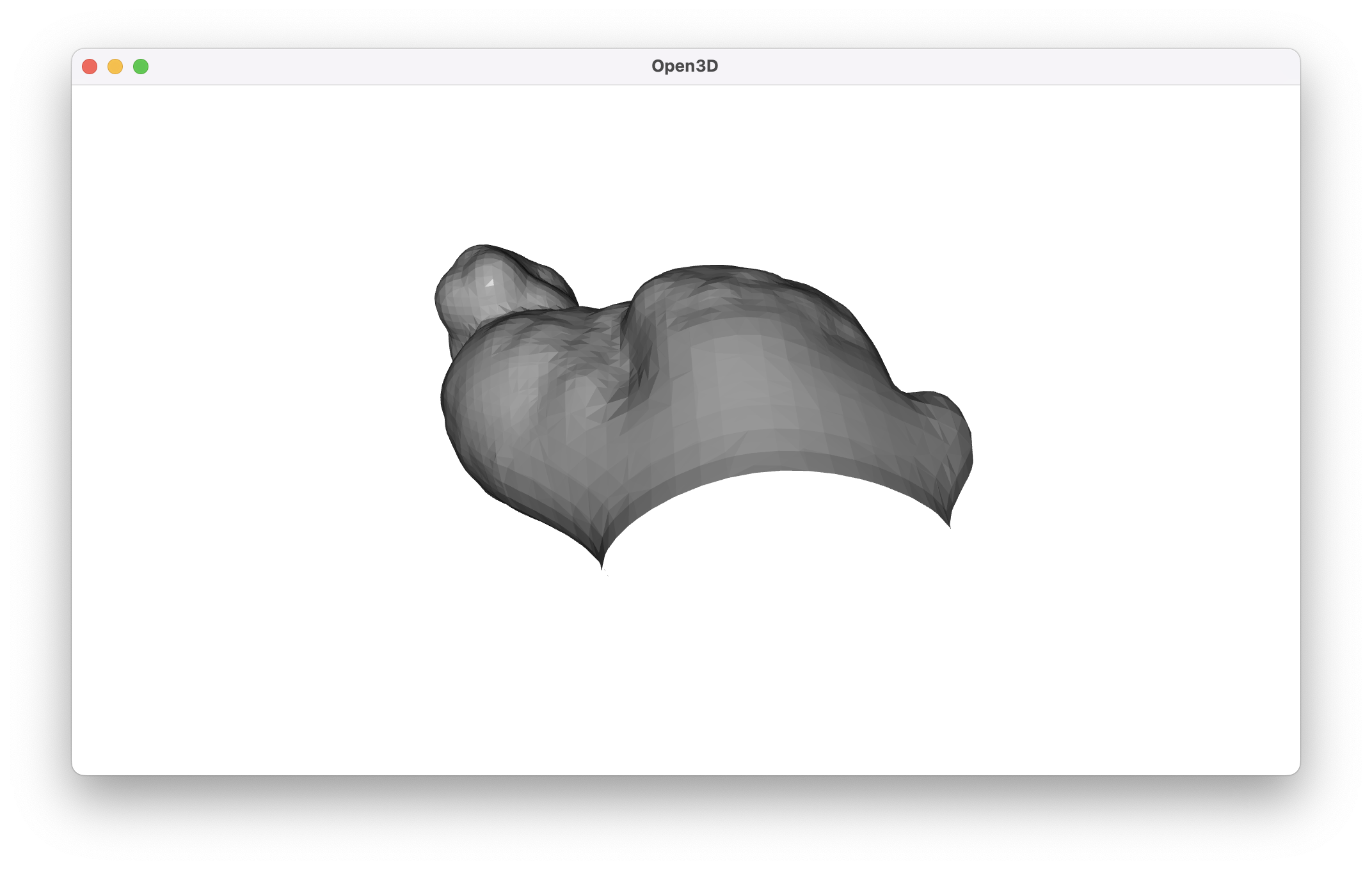
Building a Mesh with Spherical Embedding

Before we explore a very different way to build a mesh, it's worth being aware that in practice we can correct the gaps that we're seeing using a post-processing strategy like MeshFix.³ This is almost certainly going to result in a higher-quality final product than what we're about to discuss. Alternatively, the original Poisson surface reconstruction paper in 2006 has seen additional improvements since then that can be used to solve this exact problem. As such, it may be possible to use the library that the authors maintain to force the final mesh to be topologically equivalent to a sphere. Still, it's interesting to explore alternative methods that guarantee a particular type of output.

With those caveats out of the way, this 2004 paper proposes a different way to form a mesh for a genus-0 surface.⁴ The process is as follows:

1. Precompute the k-nearest neighbors of every point.
2. Find a spherical embedding of the point cloud where each point's local neighborhood on the sphere is roughly equivalent to it's original neighborhood before embedding.
3. Compute the convex hull of this embedding.
4. Use the connected edges in the convex hull (which should contain all the original points) to determine which points should be connected in the original point cloud.

If we're still thinking in terms of the tools Open3D provides, steps one, three, and four are fairly straightforward to accomplish. The difficulty is in finding a good spherical embedding. While we can easily project points onto a sphere, naive projections can contain overlapping sections of points that shouldn't be connected in the final mesh. So, the overlapping sections need to be gradually "unfolded". As usual, it's easier to understand this problem with a visual example.

def spherify(
    pc: o3d.geometry.PointCloud,
    center: np.ndarray = np.zeros(3),
    radius: float = 1.0,
    visualize: bool = False,
) -> o3d.geometry.PointCloud:
    points = np.asarray(pc.points)
    colors = pc.colors

    # Compute distance from center for all points.
    distances = np.linalg.norm(points - center, axis=1)

    # Normalize all points so that distance from the center is
    # equal to the radius.
    spherified_points = (points.T * (radius / distances)).T

    spherified_pc = o3d.geometry.PointCloud()
    spherified_pc.points = o3d.utility.Vector3dVector(spherified_points)
    spherified_pc.colors = colors

    if visualize:
        o3d.visualization.draw_geometries([spherified_pc])

    return spherified_pc


center = bunny_pc.get_center()

# Invert the center so that it's subtracted from all of the points
# in order to move the origin to the center of the point cloud.
translated_bunny_pc = bunny_pc.translate(-center)

bunny_sphere_pc = spherify(translated_bunny_pc, radius=1, visualize=True)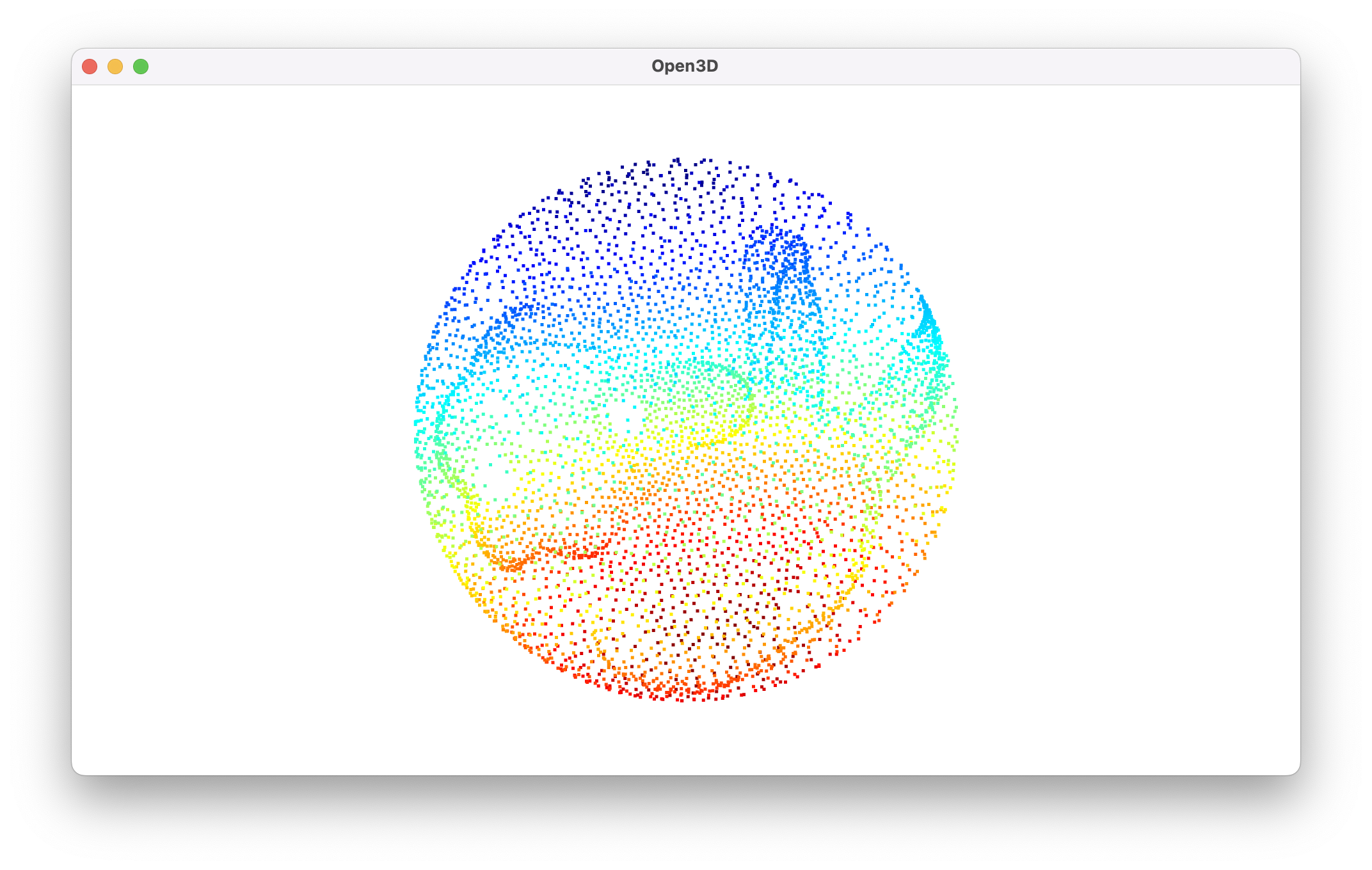

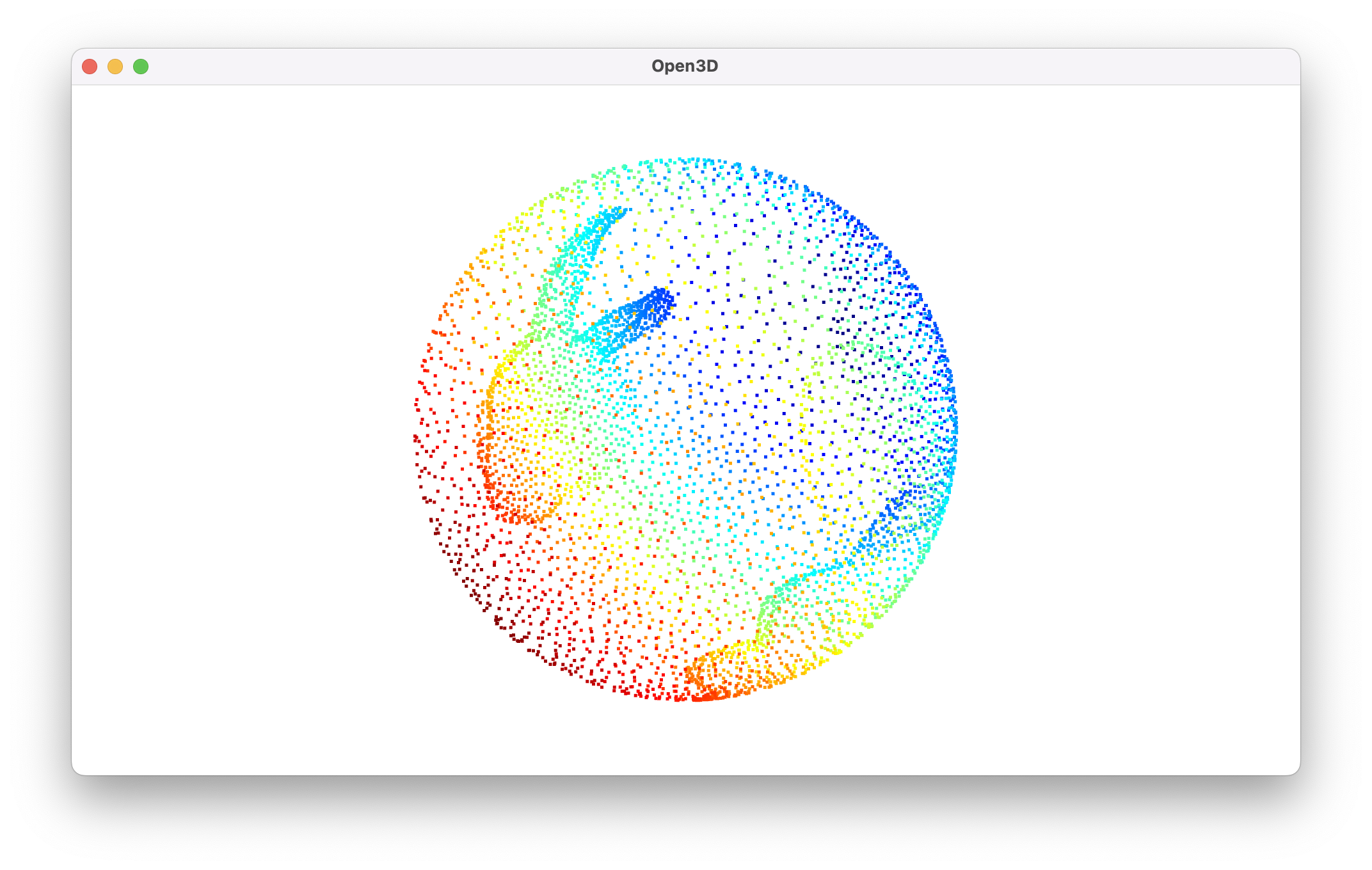
We can see that both sides of the ears of the bunny have been pressed together onto the points of its back. If we formed a mesh out of this directly, points that aren't actually near each other in the point cloud would be connected in the final output.

In fact, we can go ahead and build some of our scaffolding to form the final mesh from points on a sphere in order to visualize this. We need a function that builds a convex hull from the points on a sphere and maps the edges from the hull back to the original point cloud.

def build_mesh_from_spherified_points(
    original_pc: o3d.geometry.PointCloud,
    spherified_points: np.ndarray,
    visualize: bool = False,
) -> o3d.geometry.TriangleMesh:
    """
    Assumes that the points in the original point cloud and
    the spherified points are in the same order.
    """
    pc = o3d.geometry.PointCloud()
    pc.points = o3d.utility.Vector3dVector(spherified_points)

    # Since we've projected onto a unit sphere, this will always
    # contain all of the points.
    convex_hull_mesh, convex_hull_included_indexes = pc.compute_convex_hull()

    # Each row contains the three indexes of vertices to be connected.
    triangles = np.asarray(convex_hull_mesh.triangles)

    original_points = np.asarray(original_pc.points)

    final_mesh = o3d.geometry.TriangleMesh(
        vertices=o3d.utility.Vector3dVector(
            # Numpy trick to order reorder the original points
            # to the order given from the output of the convex
            # hull calculation.
            original_points[convex_hull_included_indexes]
        ),
        triangles=o3d.utility.Vector3iVector(triangles),
    )

    final_mesh.compute_vertex_normals()  # For shading
    final_mesh.paint_uniform_color([0.5, 0.5, 0.5])

    if visualize:
        o3d.visualization.draw_geometries([final_mesh])

    return final_mesh


# Copying to a new array fixes a strange error that I was having
# on the macOS build of Open3D.
build_mesh_from_spherified_points(
    bunny_pc, np.array(bunny_sphere_pc.points), visualize=True
)

The sides of the bunny actually look quite good just from this projection, but obviously there's still a lot of room for improvement. The authors propose a method of gradually perturbing the points until they unravel. We can summarize it in the following steps:

1. Translate all of the points so that the center of the point cloud lies on the origin.
2. Project the points onto the unit sphere.
3. Compute the Laplace-Beltrami operator for each point and add it to the point.
4. Repeat from the beginning until the Laplace-Beltrami operators for each point are close to zero.

To define the Laplace-Beltrami operator, we need a few additional definitions. We'll define p_i to be point i in the original point cloud, N_i to be the set of indexes of the k-nearest neighbors for p_i in the original point cloud, and u_i to be point formed by projecting p_i onto the unit sphere. The Laplacian L_i of u_i is approximated by the following formula.⁵

L_i = \sum_{j \in N_i} w_{ij} (u_j - u_i)

Intuitively, this is a way of having each of the neighbors of u_i "pull" toward themselves. The Laplacian is the weighted sum of the vectors representing those "pulls". Neighbors who are farther away pull harder, and the hope is that this results in the kind of unwrapping that we're hoping to see.

The Laplace-Beltrami operator L^*_i is defined in the paper as the part of the Laplacian that lies along the plane tangent to the unit sphere at point u_i. To get that tangential component, we project the Laplacian onto the unit vector pointing from the sphere center (in this case, the origin) to u_i. Then, we can subtract that from L_i to get a vector facing the correct direction. Let \hat{u} be the vector u_i - \mathbf{0}. Then, the formula to compute the Laplace-Beltrami operator for a point u_i on the sphere is the following.

L^*_i = L_i - (L_i \cdot{} \hat{u})\, \hat{u}

With this final component, we have what we need to actually implement the spherical embedding part of the algorithm.

Computing the Spherical Embedding

We can begin by slightly modifying the way that we project points in the spherify() function. We want our data to stay in numpy arrays as much as possible to minimize the amount of time we have to spend copying from one data format to another.

def spherify_array(
    points: np.ndarray, center: np.ndarray = np.zeros(3), radius: float = 1.0
) -> np.ndarray:
    """
    Expects points in an array with shape (n, 3).
    """
    # Compute distance from center for all points.
    distances = np.linalg.norm(points - center, axis=1)

    # Normalize all points so that distance from the center is
    # equal to the radius.
    spherified_points = (points.T * (radius / distances)).T

    return spherified_points

Next, we'll write a function that pre-computes every point's k-nearest neighbors.⁶ We'll store these as lists of indexes in order to make use of a bit of numpy trickery later on.

def build_neighboring_index_array(
    pc: o3d.geometry.PointCloud, num_neighbors: int = 10
) -> np.ndarray:
    k = num_neighbors + 1  # knn first returns the point, itself.

    # Get the neighbors for each vertex.
    tree = o3d.geometry.KDTreeFlann(pc)
    neighboring_index_list = []
    points = np.asarray(pc.points)

    for point in points:
        # Be aware that this is incompatible with numpy 2. Reducing
        # to 1.26.4 fixed a segfault issue.
        _, indexes, _ = tree.search_knn_vector_3d(point, k)
        neighboring_index_list.append(indexes[1:])

    return np.array(neighboring_index_list)

The final function is the most complex. We need to compute the Laplace-Beltrami operator for each point at each iteration. Some of the numpy operations in this function are less than intuitive, but the goal is to perform operations on all points simultaneously. Iterating through each point would be significantly slower.

def find_spherical_embedding(
    points: np.ndarray,
    neighboring_indexes: np.ndarray,
    num_iterations: int = 1000,
    damping_coefficient: float = 0.5,
) -> np.ndarray:
    number_of_points = len(points)

    # Make a copy of the points to work with.
    working_points = np.array(points)

    for _ in range(num_iterations):
        # Move the center of the points to the origin.
        center = np.average(working_points, axis=0)
        translated_points = working_points - center

        # Project the points onto the unit sphere.
        spherified_points = spherify_array(translated_points)

        # This effectively replaces each index in the neighboring
        # indexes list with the actual point at that index.
        neighboring_points = spherified_points[neighboring_indexes]

        # For each neighboring point u_j of u_j, compute u_j - u_i.
        neighboring_differences = neighboring_points - spherified_points.reshape(
            number_of_points, 1, 3
        )

        # Get the weighted sum of the differences.
        laplacians = np.average(neighboring_differences, axis=1)

        # Compute the dot product of each laplacian with its
        # corresponding point u_i.
        dots = np.sum(laplacians * spherified_points, axis=1)

        # Compute the Laplace-Beltrami operators for all points.
        lbs = laplacians - (spherified_points.T * dots).T

        # Perturb each point based on its Laplace-Beltrami operator.
        perturbed_points = spherified_points + damping_coefficient * lbs

        # Get ready to go around again. The paper includes another
        # normalization step, but that isn't really necessary.
        working_points = perturbed_points

    return working_points

It's worth noting that although the stated goal in the paper is to perturb until the Laplace-Beltrami operators reach \mathbf{0}, the authors admit that in practice, we simply have to choose the number of iterations that gives us the quality that we're looking for. Thus, we don't have any other exit condition in the code, either. Additionally, the authors apply a damping coefficient on the Laplace-Beltrami operators before adding them to the points' current positions.

Since we've broken everything down into neat pieces, the final function that ties everything together is very simple.

def spherically_meshify(
    pc: o3d.geometry.PointCloud,
    num_iterations: int = 1000,
    num_neighbors: int = 25,
    damping_coefficient: float = 0.5,
    visualize: bool = False,
) -> o3d.geometry.TriangleMesh:
    neighboring_indexes = build_neighboring_index_array(pc, num_neighbors)

    spherical_embedding_points = find_spherical_embedding(
        np.array(pc.points),
        neighboring_indexes,
        num_iterations=num_iterations,
        damping_coefficient=damping_coefficient,
    )

    final_mesh = build_mesh_from_spherified_points(
        pc, spherical_embedding_points, visualize=visualize
    )

    return final_mesh

The default values are set based on values in the paper. From here, all that's left is to run a few experiments to see what the performance is like. We can run a series of tests that show how the embedding is gradually refined over time.

for n in [1, 10, 100, 1000]:
    spherically_meshify(
        bunny_pc,
        num_iterations=n,
        num_neighbors=25,
        visualize=True,
    )

It's especially interesting to see how the ears of the bunny begin to separate from its back. It makes sense that this part of the point cloud would take the most time to improve given how much overlap has to be corrected. Unfortunately, it seems like we reach a point where increasing the number of iterations doesn't continue to refine the mesh by very much.

spherically_meshify(
    bunny_pc,
    num_iterations=10_000,
    num_neighbors=25,
    visualize=True,
)

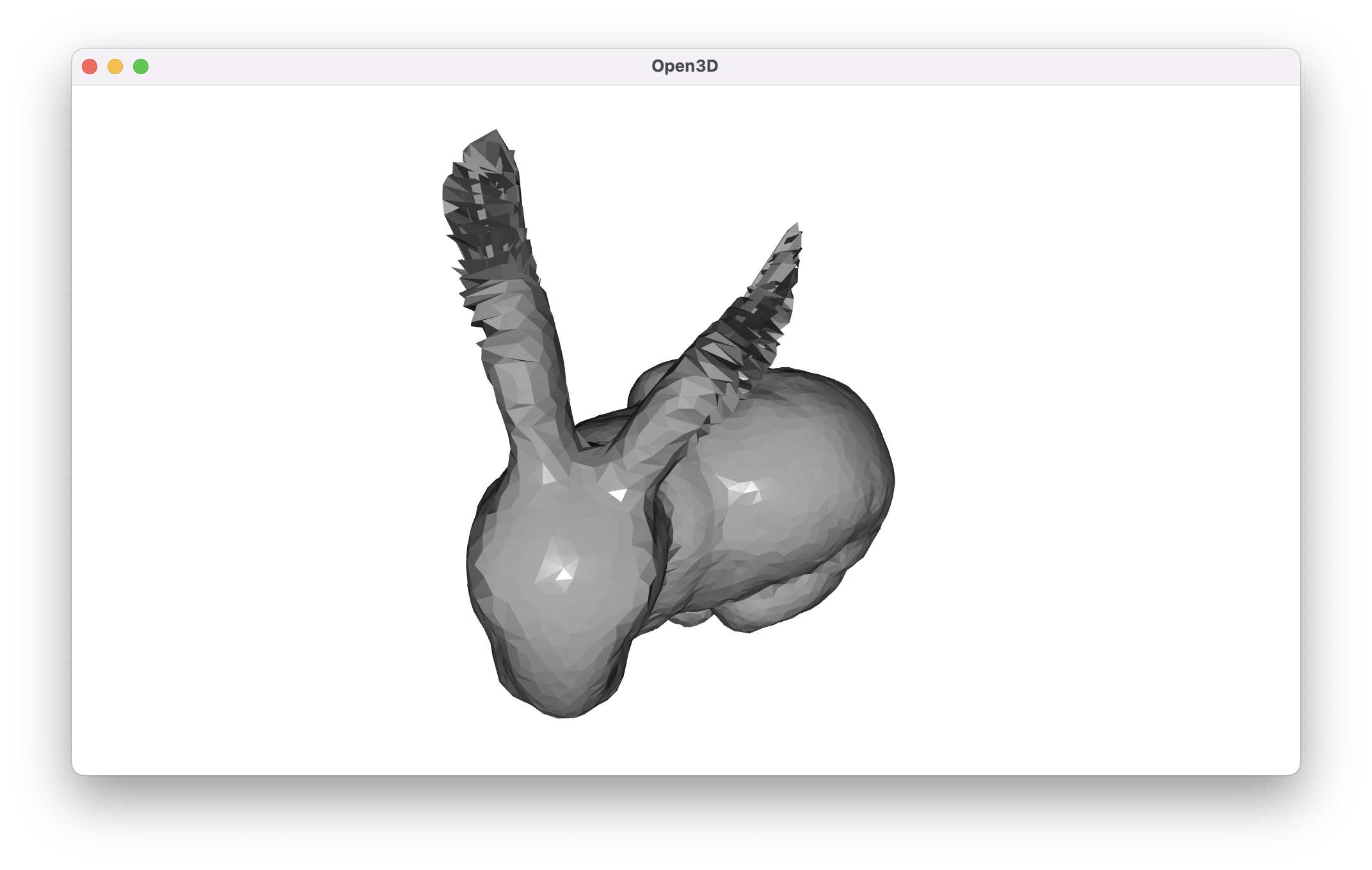
At ten thousand iterations, we've still improved slightly, but not as much as we would hope. At this point, as well, the time taken to generate this mesh is starting to drift upward from "perceptible" to "slow". For context, on an M1 macbook pro, Poisson surface reconstruction seems to take about half a second. The ten-thousand-iteration run of finding a spherical embedding is taking closer to thirty seconds.

We can instead try to alter some of the other parameters to improve the quality of the final mesh, but that's also one of the selling points of an algorithm like Poisson surface reconstruction. There's very little fiddling that's necessary to get good results.

Increasing the number of neighbors we consider is generally a losing strategy because we might accidentally pull towards the other side of the bunny's ear. We can also increase the damping coefficient so that the effect of the Laplace-Beltrami operator is more pronounced, but this also isn't a panacea. Even if we crank up the number of iterations to a particularly high value like one hundred thousand, we still don't eliminate some of the jaggedness and self-intersection present in the ears. Granted, because of the way we've constructed this mesh, Open3D does report that it is orientable, edge manifold, and vertex manifold. However, the self-intersections mean that it isn't watertight and certainly isn't an accurate representation of the real world.

mesh = spherically_meshify(
    bunny_pc,
    num_iterations=1_000,
    num_neighbors=25,
)

print(f"Orientable: {mesh.is_orientable()}")
print(f"Self-intersecting: {mesh.is_self_intersecting()}")
print(f"Edge Manifold: {mesh.is_edge_manifold()}")
print(f"Vertex Manifold: {mesh.is_vertex_manifold()}")
print(f"Watertight: {mesh.is_watertight()}")

Orientable: True
Self-intersecting: True
Edge Manifold: True
Vertex Manifold: True
Watertight: False

We can achieve slightly better results by significantly increasing the number of points that we sample from the original bunny mesh, but that's only a strategy that can be employed by someone who already has an excellent mesh. That makes it effectively useless in a real-world situation, especially when working with pre-recorded point clouds. It's still worth noting, however, that this algorithm may perform better in cases where the point density is higher.

Limitations notwithstanding, we can take a look at what happens when running against the cropped bunny point cloud to see that we do still retain the advantage of forcing a hole-free output.⁷

mesh_from_cropped = spherically_meshify(
    cropped_bunny_pc,
    num_iterations=10_000,
    num_neighbors=25,
    visualize=True
)

Conclusion

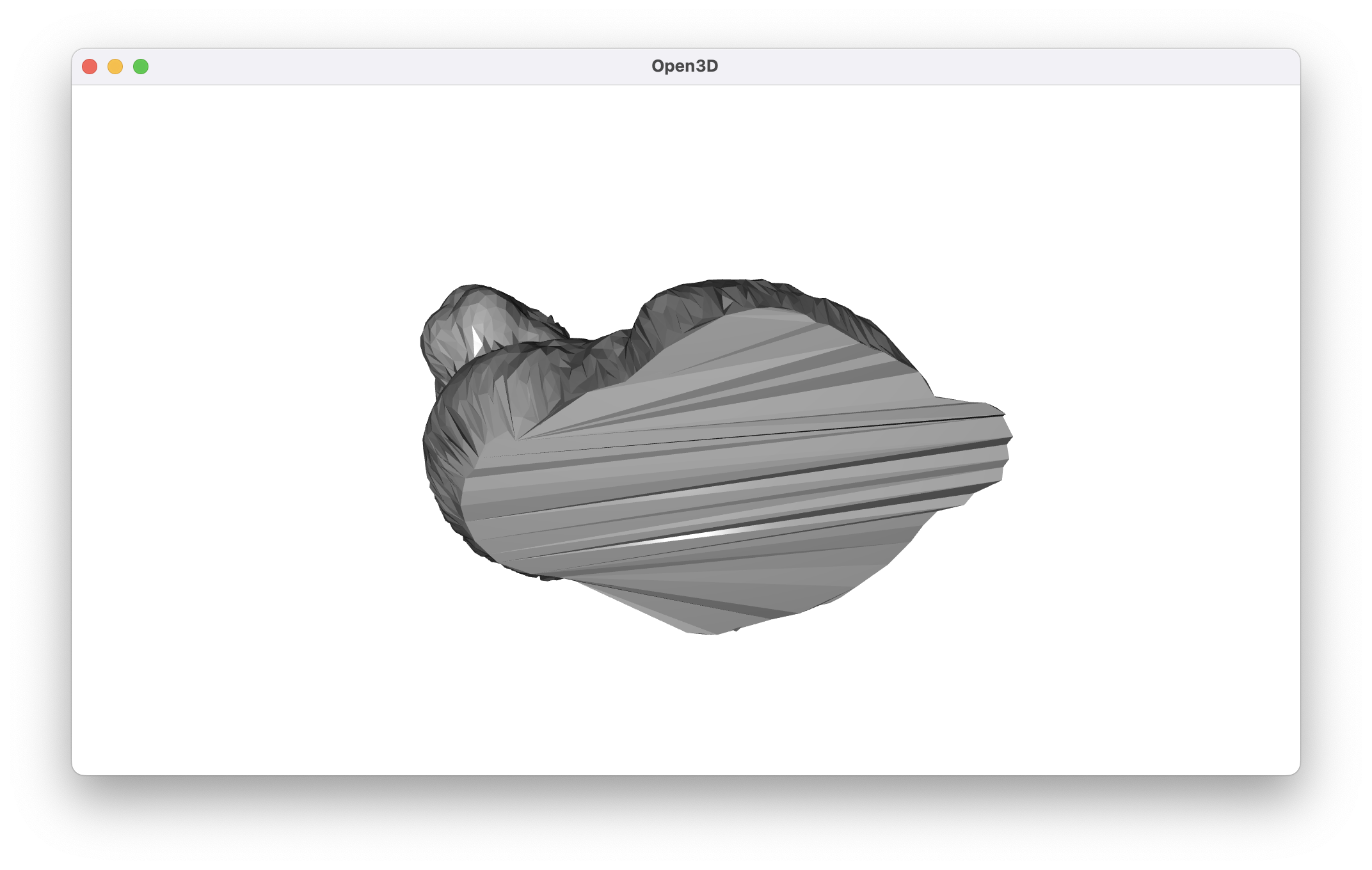
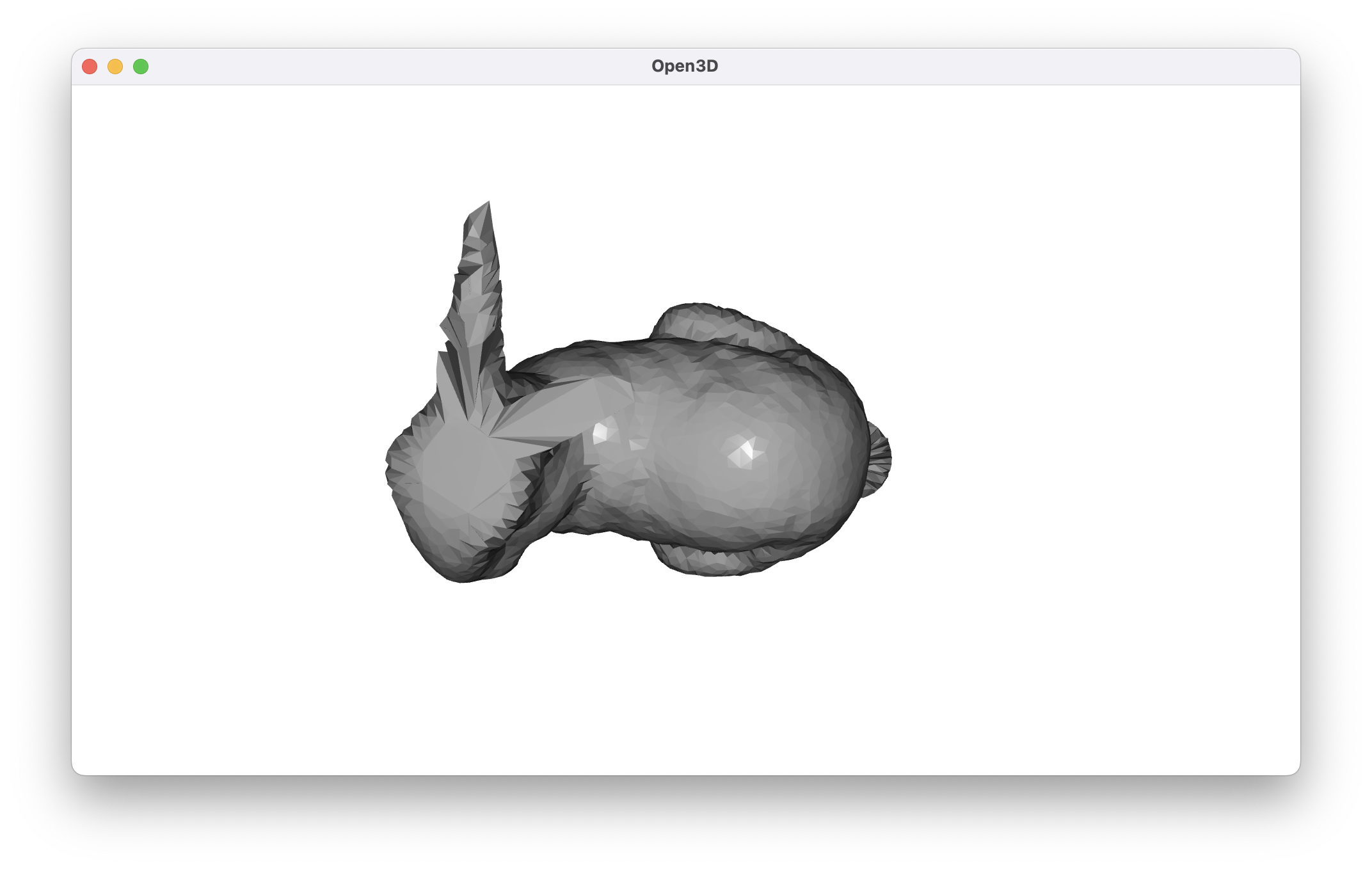
The primary advantage of an algorithm like this is in guaranteeing that the output mesh has no gaps. For very simple objects, it may even be possible to form a good mesh from projection directly or after just a few iterations of refinement. In the general case, however, the spherical meshing algorithm needs to be more aggressive in unwrapping regions of the point cloud that are close together. There isn't really a mechanism for having points not near each other in the original point cloud push away from each other on the sphere. Further, it seems like the choice of center point for the initial projection is too important. It's unlikely that we would see good results if we didn't choose a point inside the object, and there are certainly objects which are topologically equivalent to a sphere whose centroid lies on the outside of the object's surface.

What might be helpful would be to use the oriented points from the original Poisson surface reconstruction paper to have more of a "ballooning" strategy which pushes outward toward a spherical embedding. We might be able to push the points in combination with this orientation information in a way that assures that even thin sections are spread evenly over the sphere's surface.

Please try the code, which generates exactly the same collection of outputs as what is seen in the screenshots given above, and feel free reach out to discuss errors or additional thoughts.